9.3 KiB
| Home → Tutorial Home → Dynamic Events |
|---|
Dynamic Events - Making Contact
Contents
- What are Dynamic Events?
- Dynamic Event Jobs
- Specifying an Event Boundary
- Calling regula_falsi()
- Updating Our Cannonball Simulation
What are Dynamic Events?
Our numerical cannon ball simulation still needs to determine the precise time of impact, t when y(t)=0.
Remember that the reason for using numerical methods is that simulations often don't have analytical solutions. So, even though we do have an expression that will immediately tell us the time of impact of our cannon ball, we're going to pretend, for now, and for the sake of this tutorial, that we don't.
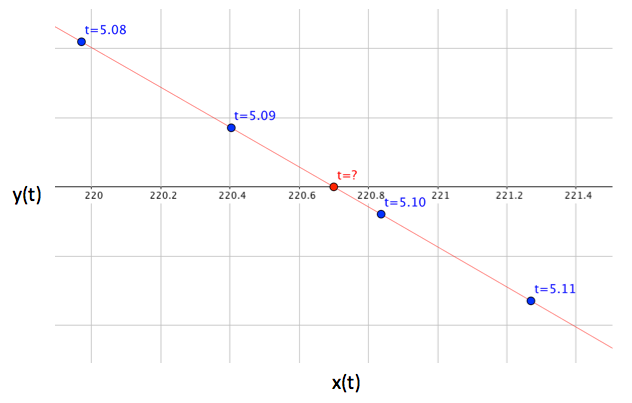
Let's take a look at the plot of the cannon ball trajectory near y(t)=0, in the figure below. Each blue point represents the state of the cannon ball at the indicated time step.
Notice that the ball's trajectory crosses y(t)=0 (the ground) in between our time steps, somewhere between 5.09 seconds, and 5.10 seconds. So, the question is, how do we find the exact time that it crosses the y-axis? In Trick, we call this type of occurrence, when our simulation state is at some boundary that we've defined, a dynamic-event. To find dynamic-events, we use dynamic-event jobs.
Figure - Cannon Ball Trajectory Near y(t) = 0
Dynamic Event Jobs
A dynamic-event job is called periodically, after each integration step.
Its job is to detect when the simulation state crosses a user-defined
event boundary, to take control of integration to find the exact event state
and time, and finally to perform some action as a result. It does
this using the Trick's regula_falsi() function and REGULA_FALSI
data-type to implement the
False position method.
Finding Events with regula_falsi()
The regula_falsi() function is the heart of a dynamic event function.
It's job is to:
- monitor the simulation state produced by each integration step,
- detect when the state crosses a specified event boundary, and
- guide Trick's integration scheduler to find that event.
Progress toward finding the event state is recorded in a REGULA_FALSI
variable.
The function cannon_impact(), listed below is the dynamic event job
function that we'll use for our cannonball simulation.
double cannon_impact( CANNON* C ) {
double tgo ; /* time-to-go */
double now ; /* current integration time. */
C->rf.error = C->pos[1] ; /* Specify the event boundary. */
now = get_integ_time() ; /* Get the current integration time */
tgo = regula_falsi( now, &(C->rf) ) ; /* Estimate remaining integration time. */
if (tgo == 0.0) { /* If we are at the event, it's action time! */
now = get_integ_time() ;
reset_regula_falsi( now, &(C->rf) ) ;
C->impact = 1 ;
C->impactTime = now ;
C->vel[0] = 0.0 ; C->vel[1] = 0.0 ;
C->acc[0] = 0.0 ; C->acc[1] = 0.0 ;
fprintf(stderr, "\n\nIMPACT: t = %.9f, pos[0] = %.9f\n\n", now, C->pos[0] ) ;
}
return (tgo) ;
}
In the following two sections, we'll discuss the details of how this and other dynamic event jobs work.
Specifying an Event Boundary
REGULA_FALSI.error
An event boundary is defined by a user-supplied error-function of the simulation
state. After each integration step, the dynamic event job evaluates the error
function at the current state and then assigns the error-value to
REGULA_FALSI.error. The REGULA_FALSI object is then passed into
regula_falsi() as an argument.
The magnitude of the error should indicate how close the given state is to the event state, and the sign of the error should indicate which side of the boundary the given state is on. An error-value of 0 should indicate that the given state is the same as the event state.
In our cannon_impact function above, the assignment
C->rf.error = C->pos[1] ; defines our cannonball's event boundary, that
is, the surface of the ground. When C->pos[1] is positive, the ball is
above the surface. When negative, it's below the surface. When zero, it's at
the surface.
REGULA_FALSI.mode
Notice that a sign change of the error-value, between consecutive states indicates that the state has crossed the event boundary. In our cannonball simulation, we only care about the situation in which the error changes from positive to negative. A situation in which the error crosses from negative to positive simply won't occur, so we don't really care. But what if we did care, because, for example, we wanted to detect when the cannon ball hit a ceiling?
The enumeration member variable REGULA_FALSI.mode allows us to specify
the crossing directions in which we are interested. Possible are values :
- Any - (default) specifies that an event occurs when the boundary is crossed from either direction, that is, from positive to negative or from negative to positive.
- Increasing - specifies that an event occurs only when the boundary is crossed from negative to positive.
- Decreasing - specifies that an event occurs only when the boundary is crossed from positive to negative.
So, in our cannon ball simulation, we could set C->rf.mode to
Decreasing to explicitly indicate that the only events we care about are
positive to negative boundary crossings. Or, we could just let the mode default
to Any, because the cannonball doesn't start below the ground.
REGULA_FALSI.error_tol
To specify the how small the error should be before declaring success, set
REGULA_FALSI.error_tol. The default error tolerance is 1.0e-15.
Calling regula_falsi()
Given the current integration time, from get_integ_time(), and a pointer
to the REGULA_FALSI variable, regula_falsi() returns an estimate
of amount of integration time necessary to reach the event.
When the estimate (tgo in our example) is equal to 0.0, we've found the event. At this point, the actions meant to result from the event should be performed.
In the action block, the first thing you'll want to do is the get the current
simulation time. This is the event time. Then you'll want to reset the
REGULA_FALSI object to it's default state with reset_regula_falsi().
After do whatever needs to happen as a result of the event. In
our cannon ball simulation, we want the ball to stop moving when it hits the
ground. So, we set its state-derivatives to zero.
If we had wanted our ball to bounce instead of just stopping, we could instead have changed the balls velocity vector to account for the rebound, and energy loss.
Regardless of its value, the time estimate is returned by the dynamic event job, to the Trick integration scheduler to let it know what its next integration step size should be.
When the dynamic event job returns 0.0, the integration scheduler will return to its normal behavior of integrating from the current state to the next integer multiple of the integloop time step.
Updating Our Cannonball Simulation
Step 1 - Modifications to cannon.h
To the #include directives near the top of the file, add:
#include "trick/regula_falsi.h"
then add the following new member to the CANNON struct :
REGULA_FALSI rf ;
Step 2 - Modifications to cannon_numeric.h
Add the following prototype for our new dynamic event job function, cannon_impact below the existing cannon_deriv prototype.
double cannon_impact(CANNON*) ;
Step 3 - Modifications to cannon_numeric.c
Add the cannon_impact function, listed above, to the bottom of cannon_numeric.c.
Step 4 - Modifications to SIM_cannon_numeric/S_define
Add the following job specification, to run our cannon_impact job.
("dynamic_event") cannon_impact( &cannon ) ;
to the end of the list of jobs in the CannonSimObject.
Step 5 - Build the Simulation
cd to the SIM_cannon_numeric directory, and type:
trick-CP to build or re-build the simulation.
If all goes well, you should see:
Trick Build Process Complete
Step 6 - Run the Simulation
Execute the Simulation:
./S_main_Darwin_16.exe RUN_test/input.py
You should see:
IMPACT: t = 5.096839959, pos[0] = 220.699644186
========================================
Cannon Ball State at Shutdown
t = 5.2
pos = [220.699644186, 0.000000000]
vel = [0.000000000, 0.000000000]
========================================
It's the same answer we got from our analytic simulation!