9.8 KiB
Control
Contents
class DifferentialDriveController
Description
The DifferentialDriveController controls the wheelbot's two drive motors so that it moves at a desired speed and heading.
The vehicle's heading-rate (𝜓̇), and speed, or range-rate (V) are both functions of the left and right wheel speeds (radians/sec). We also need the radius of the wheels (R), and the distance between the wheels (D).
| Access | Member Name | Type | Units | Value |
|---|---|---|---|---|
| private | distanceBetweenWheels | double | m | Constructor Parameter |
| private | wheelRadius | double | m | Constructor Parameter |
We're also constrained by the limitations of the motors, the vehicle, and the requirements of our design. Motors for example will be limited in speed.
| Access | Member Name | Type | Units | Value |
|---|---|---|---|---|
| private | wheelSpeedLimit | double | rad/s | Constructor Parameter |
Allocating Wheelspeed to Forward Movement and Turning
The wheel speed limit, and equations #1 and #2, above mean that there's a trade off between turning rate and speed. At maximum forward speed, the wheel speeds will be the same, and we won't be able to turn. Also, the more quickly we want to turn, the more we have to slow down. So, we have to determine how we are going to "allocate" available wheel speed to turning and moving the vehicle.
Heading Rate Determination
First, we'll determine our desired heading rate. We'll make it proportional to the heading error (the difference between our desired heading and our actual heading), and subjected to a heading rate limit.
desiredHeadingRate = headingctrl.getOutput(headingRateLimit, heading_err);
| Access | Member Name | Type | Units | Value |
|---|---|---|---|---|
| private | headingRateLimit | double | rad/s | Constructor Parameter |
| private | desiredHeadingRate | double | rad/s | determined by Heading Rate PID controller |
Apportioning the Wheel Speed Limit
Given our desired heading rate (Eq#1), we can determine the wheel-speed difference needed to achieve that.
Because half of the difference is above the average, and half is below, half of the difference will be "allocated" from the wheelSpeedLimit for turning, with the remainder allocated to moving:
-
[Eq#4] wheelSpeedForHeadingRate = (desiredHeadingRate * distanceBetweenWheels) / (2.0 * wheelRadius)
-
[Eq#5] availableWheelSpeedForRangeRate = wheelSpeedLimit - ||wheelSpeedForHeadingRate||
Range Rate Determination
With availableWheelSpeedForRangeRate determined, we can figure our range rate. Within a "slow-down distance" of a destination, we'll make it proportional to the distance error, otherwise it will be equal to our maximum available speed.
if (distance_err > slowDownDistance ) {
wheelSpeedForRangeRate = availableWheelSpeedForRangeRate;
} else {
wheelSpeedForRangeRate = wheelspeedctrl.getOutput(availableWheelSpeedForRangeRate, distance_err);
}
desiredRangeRate = wheelSpeedForRangeRate * wheelRadius;
| Access | Member Name | Type | Units | Value |
|---|---|---|---|---|
| private | slowDownDistance | double | m | Constructor Parameter |
| private | desiredRangeRate | double | m/s | Range Rate PID controller |
Calculating the Required Motor Speeds
Now that we've apportioned the available wheel speed to turning and moving, we can figure our right and left wheel speeds:
-
[Eq#6] desiredRightWheelSpeed = wheelSpeedForRangeRate + wheelSpeedForHeadingRate
-
[Eq#7] desiredLeftWheelSpeed = wheelSpeedForRangeRate - wheelSpeedForHeadingRate
Here, wheel speed is positive forward, and negative is backwards. For the motor models positive is counter clockwise, and negative is clockwise. So, we have to change sign for the right motor:
- [Eq#8] rightMotorSpeedCommand = -desiredRightWheelSpeed
- [Eq#9] leftMotorSpeedCommand = desiredLeftWheelSpeed
| Access | Member Name | Type | Units | Value |
|---|---|---|---|---|
| private | rightMotorSpeedCommand | double | rad/s | Eq#8 |
| private | leftMotorSpeedCommand | double | rad/s | Eq#9 |
Finally, we set the commanded speeds for the right and left motors:
rightMotorController.setCommandedSpeed( rightMotorSpeedCommand);
leftMotorController.setCommandedSpeed( leftMotorSpeedCommand);
| Access | Member Name | Type | Units | Value |
|---|---|---|---|---|
| private | rightMotorController | MotorSpeedController | -- | Constructor Parameter |
| private | leftMotorController | MotorSpeedController | -- | Constructor Parameter |
Constructor
DifferentialDriveController( double distanceBetweenWheels,
double wheelRadius,
double wheelSpeedLimit,
double headingRateLimit,
double slowDownDistance,
MotorSpeedController& rightMotorController,
MotorSpeedController& leftMotorController
);
Member Functions
int update( double distance_err,
double heading_err);
Determine the right and left motor speeds for the given distance, and heading errors, according to the algorithm described above.
void stop();
Stop the vehicle.
class VehicleController
Description
Constructor
VehicleController(std::vector<Point>* waypointQueue,
Navigator& navigator,
DifferentialDriveController& driveController,
double arrival_distance);
Initialize the vehicle controller instance.
-
waypointQueue- the queue of waypoints that will determine the path of the vehicle. -
navigator- pointer to an instance of the vehicle's Navigator. -
driveController- pointer to an instance of the vehicle's DifferentialDriveController.
Member Functions
int getCurrentDestination(Point& currentDestination);
Get the destination-Point to which the vehicle is currently moving. Return 0 on success, and 1 on failure.
void setWayPointQueue( std::vector<Point>* waypointQueue );
Set the queue of waypoints that will determine the path of the vehicle.
void printDestination();
Print the current destination to std::cout.
void update();
Depending on the vehicles current destination, and its distance from that destination, call the DifferentialDriveController update() method with the current distance-error, and heading-error to drive, and steer the vehicle.
void gohome();
Depending on the vehicle's homeCommanded variable, the gohome() function is called when the car needs to be homed. It sets the iterator to the last value in the waypoints list (which is set to be the home point).
bool getStatus();
Returns the status of the simulation, if it is at end with no destination then the vehicle stops moving. Used to improve end time behavior.
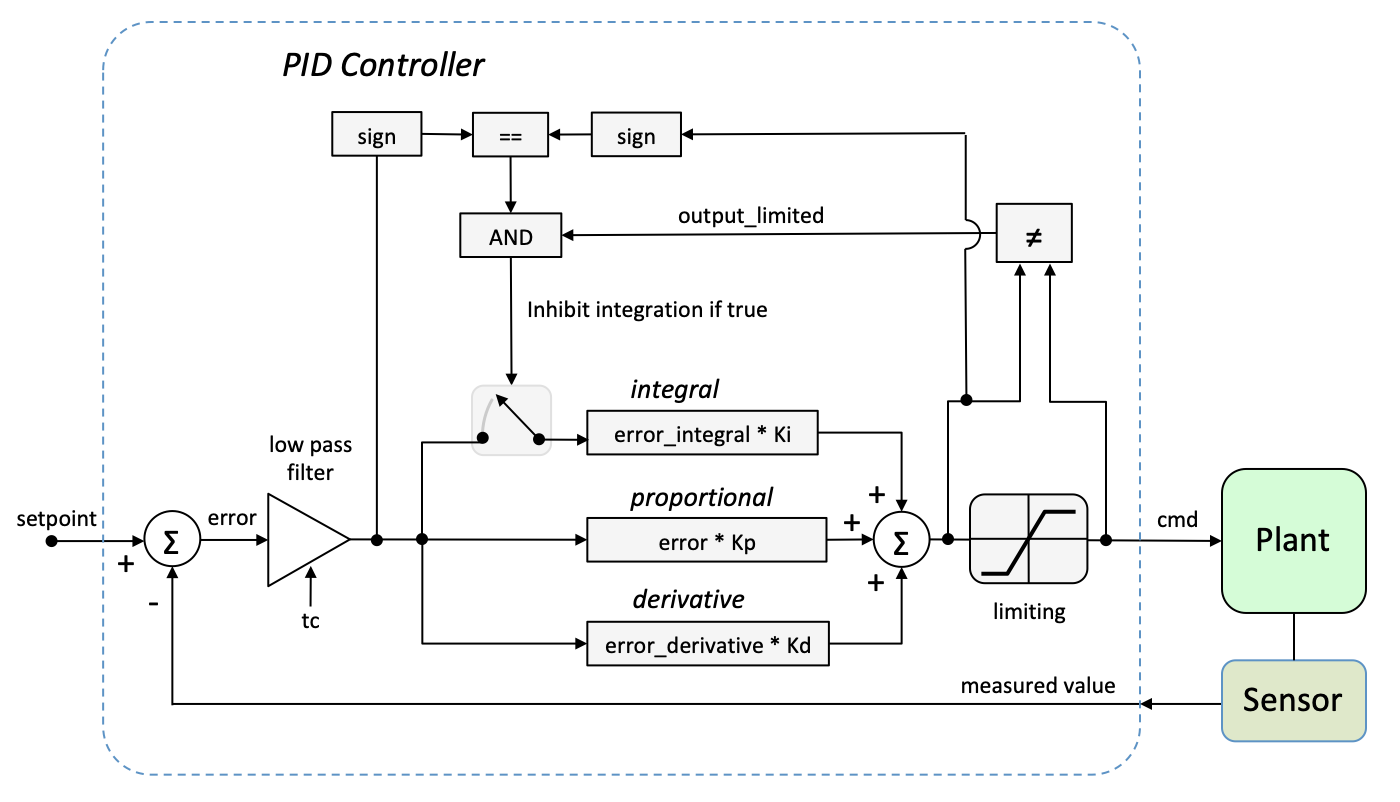
class PIDController
Constructor
PIDController::PIDController(
double kp, // proportional gain
double ki, // integral gain
double kd, // derivative gain
double omax, // limiter maximum
double omin, // limiter minimum
double dt, // sample period
double tc // filter time constant
);
For no filtering, set tc to the value of dt. To filter, set tc a value higher than dt.
double PIDController::getOutput( double setpoint_value,
double measured_value);
This function generates the control command (corresponding to cmd in the above diagram.) for the plant. The "plant" is the thing that you are controlling.
For example, the plant could be a lunar lander. The measured value could be altitude, and the command could be motor thrust. The setpoint is the what you want the output of the plant to be. The setpoint could be an altitude of 100 feet. The measured_value is the actual output (the actual altitude) of the lander plus perhaps some noise (because sensors aren't perfect).
References
The following videos provide some excellent instruction about PID control:
Understanding PID Control, Part 1: What is PID Control?
Understanding PID Control, Part 2: Expanding Beyond a Simple Integral
Understanding PID Control, Part 3: Part 3: Expanding Beyond a Simple Derivative