ExternalVendorCode/trick
1
0
Fork 0
mirror of https://github.com/nasa/trick.git synced 2024-12-28 17:08:52 +00:00
Code Issues Actions Packages Projects Releases Wiki Activity
939b3002d1
trick/trick_source/trick_utils/SAIntegrator/README.md
Penn, John M 047828115 dcf99bdf4a Editing, improvement of READMEs. #1082
2020-11-17 13:41:44 -06:00

32 KiB
Raw Blame History

Stand-Alone Integration Library

Contents

Introduction

The Stand-Alone Integration Library can be used within a Trick simulation, or independent of it.

Some examples of using these integrators can be found in the examples/ directory.

class Integrator

Description

This base-class represents a numerical integrator.

Data Members

Member Type Access Description
X_in double Protected Independent variable value of the input state.
X_out double Protected Independent variable value of the output state.
default_h double Protected Default integration step-size
user_data void* Protected A pointer to user defined data that will be passed to user-defined functions when called by the Integrator.

Constructor

Integrator(double h, void* udata);

Parameter Type Description
h double Default integration step-size
udata void* A pointer to user defined data that will be passed to user-defined functions when called by the Integrator.

Destructor

virtual ~Integrator() {}

Public Member Functions

virtual void step()

Derived classes should override this method to perform a numeric integration step, and then call advanceIndyVar() to advance the independent variable. The default behavior of this member-function is to call advanceIndyVar().

virtual void load()

Derived classes should override this method to load/prepare the integrator for the next integration step. The default behavior is to set the input value of the independent variable to its previous output value, i.e, X_in = X_out.

virtual void unload()

Derived classes should override this method to disseminate the values of the output state to their respective destinations. The default behavior is to do nothing.

virtual void integrate()

Call load(), step(), and unload() in order.

virtual double undo_integrate()

Derived classes should override this member function to undo the effect of integrate() and return that last step-size. The behavior of this function is to set the output value of the independent variable to its previous input value, i.e, X_out = X_in, and then return the default step-size default_h.

double getIndyVar()

Returns the value of the independent variable (i.e, the variable over which you are integrating) If you are integrating over time, this value will be the accumulated time.

double setIndyVar( double t)

Sets the value of the independent variable. (i.e, the variable over which you are integrating) If you are integrating over time, this will be the accumulated time.

Protected Member Functions

void advanceIndyVar()

This member function advances the independent variable by the default integration step-size.

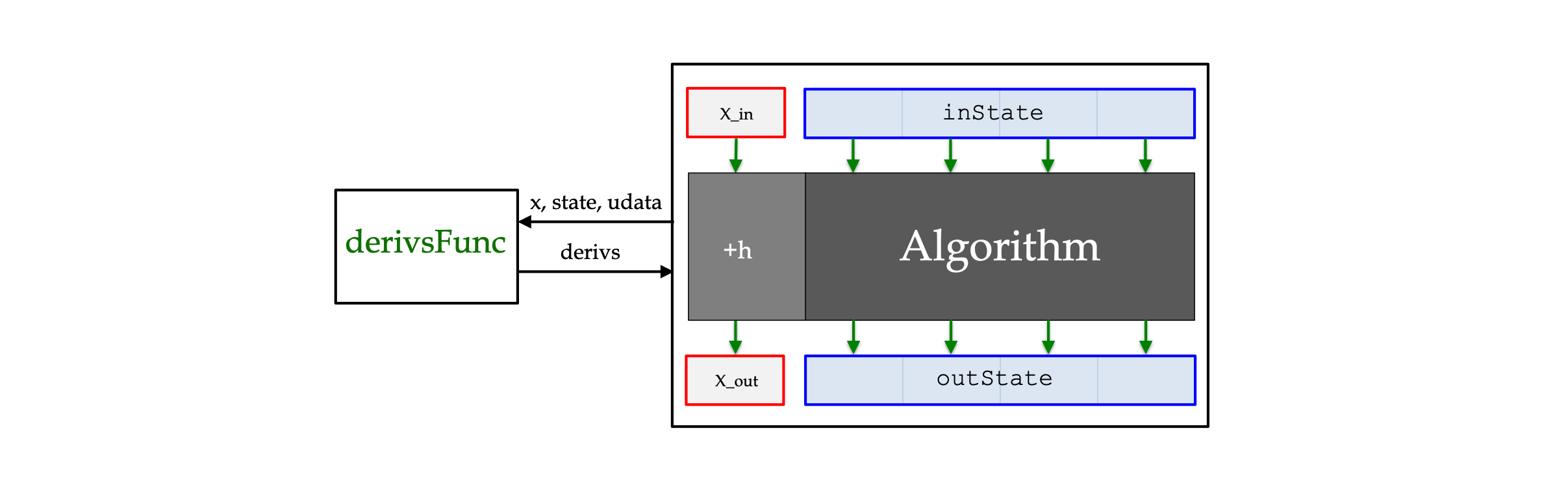
typedef DerivsFunc

Description

This typedef defines a type of C/C++ function whose purpose is to populate a state derivative array.

typedef void (*DerivsFunc)( double x, double state[], double derivs[], void* udata);

where:

Parameter Type Direction Description
x double IN Independent variable.
state double* IN Array of state variable values.
derivs double* OUT Array into which derivatives are to be returned.
udata void* IN Pointer to user_data.

Example

void my_derivs( double t, double state[], double deriv[], void* udata) { ... }

class FirstOrderODEIntegrator

Derived from Integrator.

Description

This class represents an integrator for a first order Ordinary Differential Equation.

Data Members

Those inherited from Integrator plus:

Member Type Access Description
state_size unsigned int Protected Size of the state vector.
inState double* Protected Input state vector to the integrator.
outState double* Protected Output state vector from the integrator.
inVars double** Protected Array of pointers to the variables from which input state vector values are copied.
outVars double** Protected Array of pointers to the variables to which output state vector values are copied.
derivs_func DerivsFunc Protected Function thats generates the function (an array of state derivatives) to be integrated.

This class introduces:

  • Input and output state arrays.
  • A function that calculates state-derivatives for the integration algorithm.
  • Array of pointers to variables from which to load the input state array, and array of pointers to variables to which to unload the output state array.

Constructor

FirstOrderODEIntegrator( double h,
                         int N,
                         double* in_vars[],
                         double* out_vars[],
                         DerivsFunc func,
                         void* user_data);

where:

Parameter Type Description
h double Default integration step-size.
N int Number of state variables to be integrated
in_vars double* Array of pointers to the state variables from which we load() the integrator state (in_vars and out_vars will generally point to the same array of pointers.)
out_vars double* Array of pointers to the state variables to which we unload() the integrator state (in_vars and out_vars will generally point to the same array of pointers.)
derivs_func DerivsFunc Function thats generates the function (the derivatives) to be integrated.
user_data void* A pointer to user defined data that will be passed to a DerivsFunc when called by the Integrator.

Public Member Functions

void load()

Overrides Integrator::load()

Load the integrator's initial state from the variables specified by in_vars. Set the initial value of the independent variable for the next step to the final value of the previous step. load

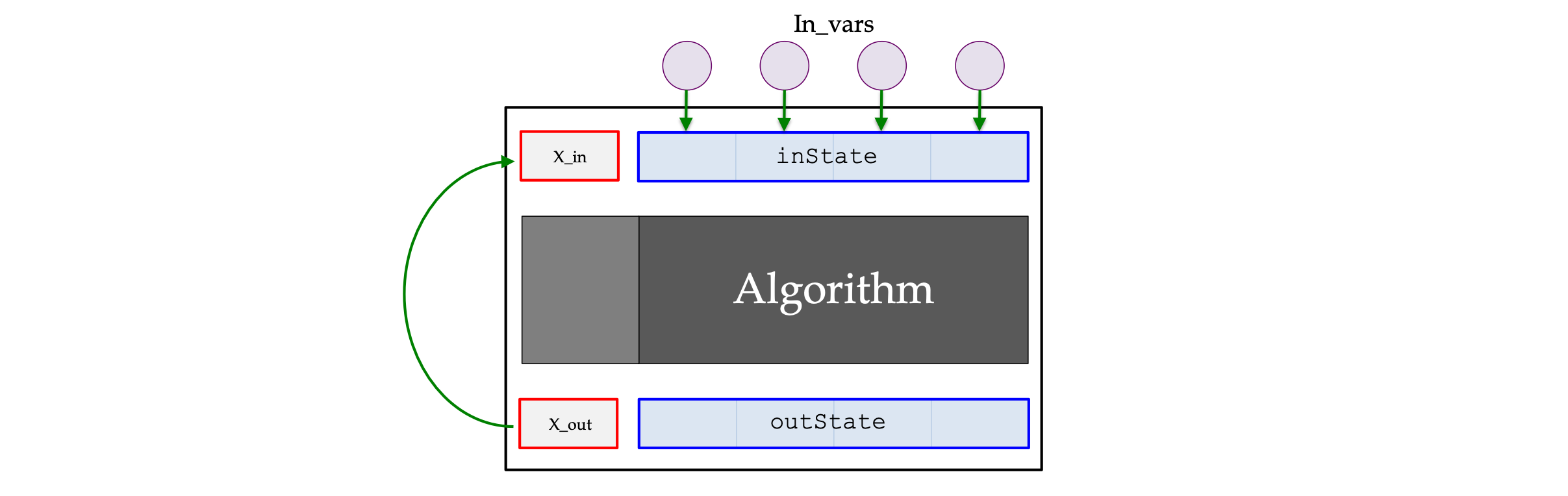
void unload()

Overrides Integrator::unload()

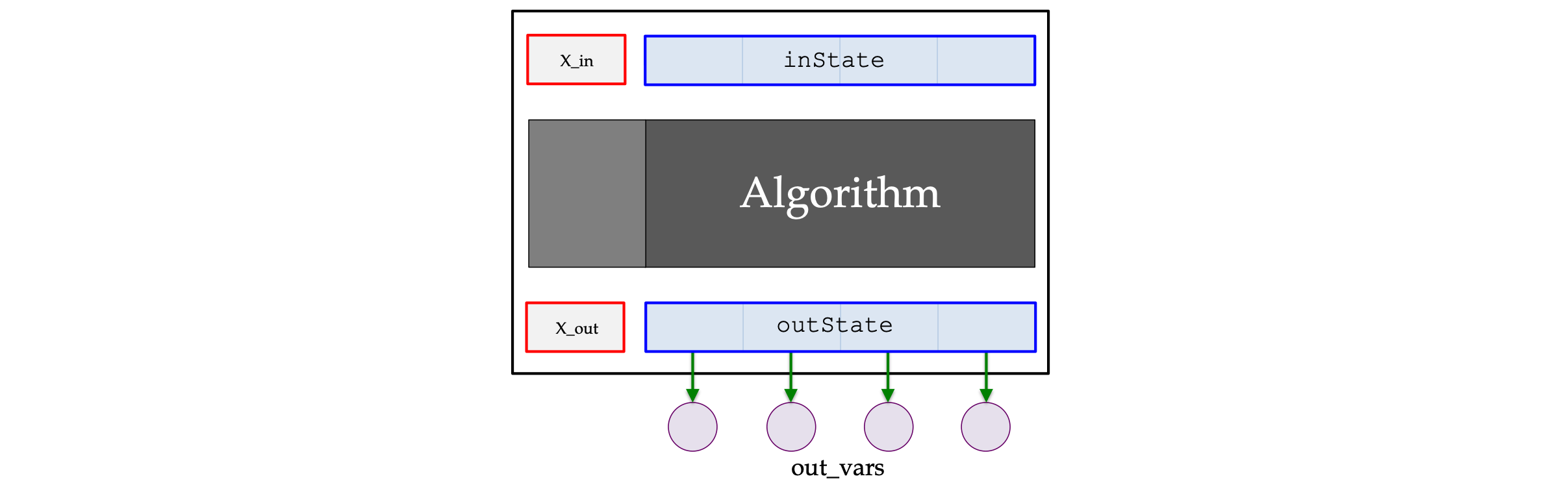
Unload the integrator's result state to the variables specified by out_vars. unload

virtual void step()

Overrides Integrator::step() step Derived classes should override this method to calculate outState using some integration algorithm, using X_in, inState, and derivs_func, and default_h. The over-riding method should also pass the user_data when calling the DerivsFunc. The default algorithm is Euler.

void integrate()

Inherited from Integrator::integrate()

virtual void undo_integrate()

Overrides Integrator::undo_integrate()

Undo the effect of the last integration step. undo_integrate

void load_from_outState()

Load inState from outState, rather than from the variables referenced by in_vars. load_from_outState

double** set_in_vars( double* in_vars[])

This function specifies the variables from which inState values are to be copied, when load() is called. The number of elements in this array must equal the number of state variables. Return a pointer to the previous array so that it can be deleted if necessary. set_in_vars

double** set_out_vars( double* out_vars[])

This function specifies the variables to which outState values are to be copied, when unload() is called. The number of elements in this array must equal the number of state variables. Return a pointer to the previous array so that it can be deleted if necessary. set_out_vars

double getIndyVar()

Inherited from Integrator::getIndyVar()

double setIndyVar()

Inherited from Integrator::setIndyVar()

Protected Member Functions

advanceIndyVar()

Inherited from Integrator::advanceIndyVar()

typedef RootErrorFunc

Description

This typedef defines a type of C/C++ function whose purpose is to specify the job of a RootFinder.

typedef double (*RootErrorFunc)( double x, double state[], RootFinder* root_finder, void* udata);

where:

Parameter Type Direction Description
x double In Independent variable
state double* In Array of state variable values
root_finder RootFinder* In Class for finding the roots of a function.
udata void* In A pointer to user_data.

A function of type RootErrorFunc should:

  1. Specify a (math) function f(x) whose roots [x : f(x)=0] the RootFinder is meant to find.
    • f(x) is usually a function of the state variables. State variables are themselves functions of x.
  2. Call root_finder->find_roots(x, y), where y = f(x). If it returns 0.0, it's found a root of f(x).
  3. Specify what to do as a result of finding a root.
  4. Return the value returned by root_finder->find_roots().

Example RootErrorFunc from the Cannonball example

double impact( double t, double state[], RootFinder* root_finder, void* udata) {
    double root_error = root_finder->find_roots(t, state[1]);
    if (root_error == 0.0) {
        root_finder->init();
        state[2] =  0.9 * state[2];
        state[3] = -0.9 * state[3];
    }
    return (root_error);
}

In this example :

  • the independent variable is t.
  • y = f(t) = state[1], that is the y (vertical) component of the cannonball position.
  • When root_finder->find_roots returns 0.0, then the result of finding the root (i.e, [t:state[1]=0]) is to "bounce" the cannon ball, by negating the y component of the velocity, and reducing the magnitude of the velocity by 10%.

class FirstOrderODEVariableStepIntegrator

Derived from FirstOrderODEIntegrator.

Description

This class represents a first order ODE integrator whose step-size can be varied.

Data Members

Those inherited from FirstOrderODEIntegrator plus:

Member Type Access Description
root_finder RootFinder* Private Pointer to a RootFinder object.
root_error_func RootErrorFunc Private Function that specifies what happens when a function-root is found.
last_h double Protected Value of h used in the last integration step.

Constructor

Public Member Functions

void load()

Inherited from FirstOrderODEIntegrator::load()

void unload()

Inherited from FirstOrderODEIntegrator::unload()

void step()

Overrides FirstOrderODEIntegrator::step()

This function calls the virtual function variable_step() (below) with the default step-size. Then, if a RootFinder has been specified using add_Rootfinder() (below), search that interval for roots .

void integrate()

Inherited from Integrator::integrate()

double undo_integrate()

Overrides FirstOrderODEIntegrator::undo_integrate()
Call FirstOrderODEIntegrator::undo_integrate(), and then return last_h.

load_from_outState()

Inherited from FirstOrderODEIntegrator::load_from_outState()

set_in_vars()

Inherited from FirstOrderODEIntegrator::set_in_vars()

set_out_vars()

Inherited from FirstOrderODEIntegrator::set_out_vars()

virtual void variable_step( double h)

Parameter Type Description
h double Integration step-size that overrides the default step-size.

Derived classes should override this method to calculate outState using some integration algorithm, given h, X_in, inState, and derivs_func. The over-riding method should also pass the user_data when calling the DerivsFunc. step

void add_Rootfinder( RootFinder* root_finder, RootErrorFunc rfunc)

Parameter Type Description
root_finder RootFinder* RootFinder object.
rfunc RootErrorFunc User supplied function whose purpose is to specify the job of a RootFinder.

Configure the integrator to find roots of state-element vs. independent-variable functions.

double getIndyVar()

Inherited from Integrator::getIndyVar()

double setIndyVar()

Inherited from Integrator::setIndyVar()

Protected Member Functions

advanceIndyVar()

Inherited from Integrator::advanceIndyVar()

class EulerIntegrator

Derived from FirstOrderODEVariableStepIntegrator.

Description

The Euler method is a first order numerical integration method. It is the simplest, explicit Runge-Kutta method.

Data Members

Those inherited from FirstOrderODEVariableStepIntegrator.

Constructor

EulerIntegrator( double h,
                 int N,
                 double* in_vars[],
                 double* out_vars[],
                 DerivsFunc func,
                 void* user_data)

Constructor Parameters are those of FirstOrderODEVariableStepIntegrator.

Public Member Functions

void variable_step( double h)

Overrides FirstOrderODEVariableStepIntegrator::variable_step()

Calculates outState from h, X_in, inState, and derivs_func, using the Euler method.

class HeunsMethod

Derived from FirstOrderODEVariableStepIntegrator.

Description

This integrator implements Heun's Method.

Data Members

Those inherited from FirstOrderODEVariableStepIntegrator.

Constructor

HeunsMethod( double h,
             int N,
             double* in_vars[],
             double* out_vars[],
             DerivsFunc func,
             void* user_data)

Constructor Parameters are those of FirstOrderODEIntegrator.

Public Member Functions

void variable_step( double h)

Overrides FirstOrderODEVariableStepIntegrator::variable_step()

Calculates outState from h, X_in, inState, and derivs_func, using the Heun's method.

class RK2Integrator

Derived from FirstOrderODEVariableStepIntegrator.

Description

RK2Integrator implements the second order, explicit, Runge-Kutta method whose Butcher tableau is as follows.

RK2_tableau

Data Members

Those inherited from FirstOrderODEVariableStepIntegrator.

Constructor

RK2Integrator( double h,
               int N,
               double* in_vars[],
               double* out_vars[],
               DerivsFunc func,
           void* user_data)

Constructor Parameters are those of FirstOrderODEIntegrator.

Public Member Functions

void variable_step( double h)

Overrides FirstOrderODEVariableStepIntegrator::variable_step()

Calculates outState from h, X_in, inState, and derivs_func, using the Runge-Kutta 2 method.

class RK4Integrator

Derived from FirstOrderODEVariableStepIntegrator.

Description

RK4Integrator implements the fourth order, explicit, Runge-Kutta method whose Butcher tableau is as follows.

RK4_tableau

Data Members

Those inherited from FirstOrderODEVariableStepIntegrator.

Constructor

RK4Integrator( double h,
               int N,
               double* in_vars[],
               double* out_vars[],
               DerivsFunc func,
               void* user_data)

Constructor Parameters are those of FirstOrderODEIntegrator.

Public Member Functions

void variable_step( double h)

Overrides FirstOrderODEVariableStepIntegrator::variable_step()

Calculates outState from h, X_in, inState, and derivs_func, using the Runge-Kutta 4 method.

class RK3_8Integrator

Derived from FirstOrderODEVariableStepIntegrator.

Description

RK3_8Integrator implements the fourth order, explicit, Runge-Kutta method whose Butcher tableau is as follows.

RK38_tableau

Data Members

Those inherited from FirstOrderODEVariableStepIntegrator.

Constructor

RK3_8Integrator( double h,
                 int N,
                 double* in_vars[],
                 double* out_vars[],
                 DerivsFunc func,
                 void* user_data)

Constructor Parameters are those of FirstOrderODEIntegrator.

Public Member Functions

void variable_step( double h)

Overrides FirstOrderODEVariableStepIntegrator::variable_step()

Calculates outState from h, X_in, inState, and derivs_func, using the Runge-Kutta 3/8 method.

class ABM2Integrator

Derived from FirstOrderODEIntegrator.

Description

The ABM2Integrator implements the second-order Adams-Bashforth-Moulton predictor/corrector method. Adams methods maintain a history of derivatives rather than calculating intermediate values like Runge-Kutta methods.

Data Members

Those inherited from FirstOrderODEIntegrator.

Constructor

ABM2Integrator ( double h,
                 int N,
                 double* in_vars[],
                 double* out_vars[],
                 DerivsFunc func,
                 void* user_data)

Constructor Parameters are those of FirstOrderODEIntegrator.

class ABM4Integrator

Derived from FirstOrderODEIntegrator.

Description

The ABM2Integrator implements the second-order Adams-Bashforth-Moulton predictor/corrector method. Adams methods maintain a history of derivatives rather than calculating intermediate values like Runge-Kutta methods.

Data Members

Those inherited from FirstOrderODEIntegrator.

Constructor

ABM4Integrator ( double h,
                 int N,
                 double* in_vars[],
                 double* out_vars[],
                 DerivsFunc func,
                 void* user_data)

Constructor Parameters are those of FirstOrderODEIntegrator.

class EulerCromerIntegrator

Derived from Integrator.

Description

EulerCromer is integration method that conserves energy in oscillatory systems better than Runge-Kutta. So, it's good for mass-spring-damper systems, and orbital systems.

Data Members

Those inherited from Integrator plus:

Member Type Access Description
nDimensions unsigned int Protected Number of dimensions in position, velocity, and acceleration vectors. Typically 1,2, or 3.
pos_p double** Protected Array of pointers to variables from which we load() and to which we unload() the position values .
vel_p double** Protected Array of pointers to variables from which we load() and to which we unload() the velocity values .
pos_in double* Protected Position input array.
vel_in double* Protected Velocity input array.
pos_out double* Protected Position output array.
vel_out double* Protected Velocity output array.
g_out double* Protected Array of accelerations returned from gderivs.
f_out double* Protected Array of velocities returned from fderivs.
gderivs DerivsFunc Protected A function that returns accelerations.
fderivs DerivsFunc Protected A function that returns velocities.

Constructor

EulerCromerIntegrator(double dt,
                      int N,
                      double* xp[],
                      double* vp[],
                      DerivsFunc gfunc,
                      DerivsFunc ffunc,
                      void* user_data)
Parameter Type Description
dt double Default time step value. Sets Integrator::default_h.
N int Sets nDimensions above.
xp double* Sets pos_p above.
vp double* Sets vel_p above.
gfunc DerivsFunc Sets gderivs above.
ffunc DerivsFunc Sets fderivs above.
user_data void* Sets Integrator::user_data.

Public Member Functions

void step( double dt)

Parameter Type Description
dt double Integration step-size that overrides the default step-size.

This function calculates pos_out and vel_out from dt, X_in, pos_in, vel_in, f_func, and gfunc using the Euler-Cromer method.

void step()

This function calls step(dt) (above) with the default step-size.

void load()

Overrides Integrator::integrate() Load the integrator's initial state from the variables specified by xp, and vp. Set the initial value of the independent variable for the next step to the final value of the previous step.

void unload()

Overrides Integrator::integrate()

Unload the integrator's result state (pos_out, and vel_out) to the variables specified by xp, and vp.

void integrate()

Inherited from Integrator::integrate()

double undo_integrate()

Overrides Integrator::undo_integrate()

Undo the effect of the last integration step.

double getIndyVar()

Inherited from Integrator::getIndyVar()

double setIndyVar()

Inherited from Integrator::setIndyVar()

Protected Member Functions

advanceIndyVar()

Inherited from Integrator::advanceIndyVar()

enum SlopeConstraint

Description

Value Meaning
Negative Require slope of the function to be negative at the root.
Unconstrained No slope constraint.
Positive Require slope of the function to be positive at the root.

class RootFinder

Description

The RootFinder class uses the Regula-Falsi method to find roots of a math function. A root is a value of x such that f(x)=0.

Data Members

Member Type Access Description
f_upper double Private Error-function value upper bound.
x_upper double Private Independent variable value upper bound.
upper_set bool Private True = bound is valid. False = not valid.
f_lower double Private Error-function value lower bound.
x_lower double Private Independent variable value lower bound.
lower_set bool Private True = bound is valid. False = not valid.
prev_f_error double Private Absolute value of the previous root function value.
f_error_tol double Private How close is close enough.
iterations int Private Number of Regula Falsi iterations.
slope_constraint SlopeConstraint Private Find roots with this slope sign.
f_slope SlopeConstraint Private Current root function slope.

Constructors

RootFinder()

Default constructor that calls void RootFinder::init() below.

RootFinder(double tolerance, SlopeConstraint constraint)

Parameter Type Description
tolerance double Error tolerance.
constraint SlopeConstraint

Public Member Functions

void init( double tolerance, SlopeConstraint constraint)

Initialize the RootFinder with the given tolerance, and SlopeConstraint.

void RootFinder::init()

Initialize the RootFinder with the method above with:

  • tolerance = 0.00000000001
  • slope_constraint = Unconstrained

double find_roots( double x, double f_error )

  • Returns DBL_MAX if no root is detected.
  • Returns 0.0 if a root is detected, and the estimated error in f(x) is within tolerance.
  • Returns an estimated correction in x if a root is detected, but the estimated error in f(x) is not within tolerance.