|
|
||
|---|---|---|
| .. | ||
| images | ||
| Modified_data | ||
| RUN_graphics | ||
| RUN_test | ||
| www | ||
| README.md | ||
| S_define | ||
| S_overrides.mk | ||
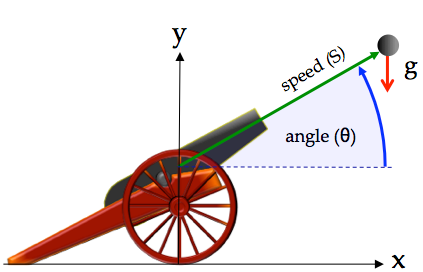
SIM_cannon_numeric
This is the second in a series example cannon ball simulations that one builds in the Trick Tutorial (Sections 9, 10). It's purpose is to introduce Trick supported numerical methods.
Rather than using the analytic solutions of SIM_cannon_analytic, this simulation uses Trick's numerical integration, and root-finding methods to:
- Determine the cannon ball state (velocity, position) at each time step, and
- Determine when and where the cannon ball impacts the ground.
The simulation is otherwise the same as SIM_cannon_analytic.
Parameterization
Same as in SIM_cannon_analytic.
Initialization
Same as in SIM_cannon_analytic.
State Propagation
This Trick simulation calculates the cannonball state by numerical integration. Acceleration is calculated in the "derivative" job cannon_deriv. It is then used in "integration" job cannon_integ to calculate the cannonball's velocity and position, using the Trick integrate function.
When and Where the Ball Impacts the Ground
The time and position of impact is determined by the "dynamic_event" event job cannon_impact, using the Trick regula_falsi function.