# SIM_splashdown
SIM_splashdown is a simulation of a space craft crew module dropping into a body of water.
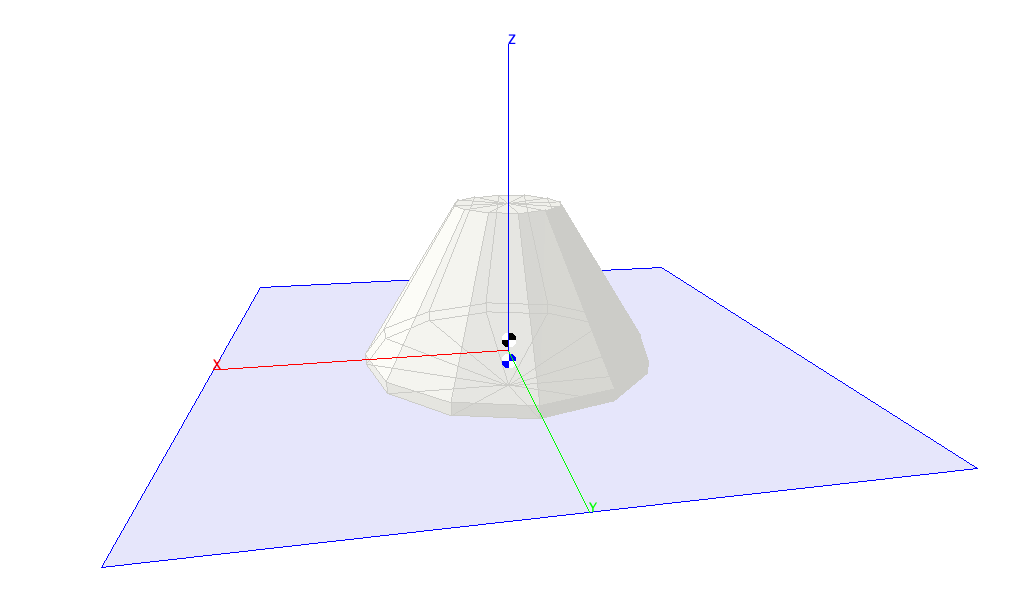
## Building the Simulation
In the ```SIM_splashdown ``` directory, type **```trick-CP```** to build the simulation executable. When it's complete, you should see:
```
=== Simulation make complete ===
```
Now **cd** into ```models/CrewModuleGraphics/``` and type **mvn package**. This builds the graphics client for the simulation.
## Running the Simulation
In the SIM_splashdown directory:
```
% S_main_*.exe RUN_test/input.py
```
The Sim Control Panel, and a graphics client called "CM Display" should appear.
Click the Start on the Trick Sim Control Panel.
Click and drag the mouse on the display to change the viewing orientation.
The black and white center of gravity symbol indicates the center of gravity of the vehicle.
The blue and white center of gravity symbol indicates the center of gravity of the water that is displaced by the vehicle, that is: the center of buoyancy.
## Dynamics Model
### Vehicle State
The vehicle state is defined by the following variables. These are calculated by numerically integrating force, velocity, torque, and body rotation rate over time.
#### Linear momentum
The linear momentum of the vehicle is determined by integrating the [total force](#total_force) on the vehicle over time.

- **```crewModule.dyn.momentum```** ( double[3] )
#### Position
The position of the vehicle is determined by integrating the [linear velocity](#linear_velocity) of the vehicle over time.

- **```crewModule.dyn.position```** ( double[3] )
#### Angular momentum
The angular momentum of the vehicle is determined by integrating the [total torque](#total_torque) of the vehicle over time.

- **```crewModule.dyn.angular_momentum```** ( double[3] )
#### Body rotation
The body rotation matrix of the vehicle is determined by integrating the [body rotation rate](#body_rotation_rate) matrix of the vehicle over time.

- **```crewModule.dyn.R```** ( double[3][3] )
### Vehicle State Derivatives and Dependencies
#### Total Force
The total force acting on the crew module is the sum of the [force of gravity](#force_of_gravity), the [force of buoyancy](#force_of_buoyancy), and the [force of drag](#force_of_drag).

- **```crewModule.dyn.force_total```** ( double[3] )
#### Force of Gravity
By Newton’s 2nd Law, the force of gravity on the vehicle is the [mass of the vehicle](#vehicle_mass) times the [acceleration of gravity](#acceleration_of_gravity).

- **```crewModule.dyn.force_gravity```** ( double[3] )
#### Acceleration of Gravity
In this simulation the acceleration is fixed at:

#### Vehicle Mass
Default value of the vehicle mass is:

- **```crewModule.dyn.mass_vehicle```** ( double )
#### Force of Buoyancy
Buoyancy is a force on an object, that opposes gravity, by a fluid within which it’s immersed. This force is equal to the [mass of the displaced water](#displaced_mass) times the [acceleration of gravity](#acceleration_of_gravity).

- **```crewModule.dyn.force_buoyancy```** ( double[3] )
#### Drag force
This drag force is not accurate. It's simply opposes the [linear velocity](#linear_velocity), as a means of sapping energy from the system.

- **```crewModule.dyn.force_drag```** ( double[3] )
#### Displaced Mass
The displaced mass of the water is equal to the [density of water](#density_of_water) times its [displaced volume](#displaced_volume).

- **```crewModule.dyn.mass_displaced```** (double)
#### Density of Water
Default value is the density of sea water:

- **```crewModule.dyn.density_of_water```** (double)
#### Total Torque
The total torque acting on the crew module is the sum of the [buoyancy torque](#buoyancy_torque), and [drag torque](#drag_torque).

- **```crewModule.dyn.torque_total```** (double[3])
#### Buoyancy Torque
The [force of buoyancy](#force_of_buoyancy) acts on the [center of buoyancy](#center_of_buoyancy), that is: the center of mass of the displaced water. So the torque on the vehicle due to buoyancy is:

- **```crewModule.dyn.torque_buoyancy```** (double[3])
#### Drag Torque
We won't even pretend this drag torque is accurate. It's simply opposes the [angular velocity](#angular_velocity), as a means of sapping energy from the system, to settle the rocking of the crew module.

- **```crewModule.dyn.torque_drag```** (double[3])
#### Angular Velocity
The angular velocity of the vehicle is a function of the [angular momentum](#angular_momentum), the vehicle [inertia tensor](#inertia_tensor) and the [vehicle body rotation](#body_rotation).

where:

- **```crewModule.dyn.angular_velocity```** (double[3])
#### Body Rotation Rate
The body rotation rate is the product of the skew-symetric-matrix form of the [angular velocity](#angular_velocity), and the [body rotation](#body_rotation) matrix.

- **```crewModule.dyn.Rdot```** (double[3][3])
#### Linear Velocity
The linear velocity of the vehicle is the [linear momentum](#linear_momentum) of the vehicle divided by its [mass](#vehicle_mass).

- **```crewModule.dyn.velocity```** (double[3])
#### Inertia Tensor
Default value is:

- **```crewModule.dyn.I_body ```** (double[3][3])
---
The following convenience function:
**```crewModule.dyn.init_inertia_tensor(double A, double B, double C);```**
sets the diagonal elements as follows:
```
I_body[0][0] = mass_vehicle * (B*B + C*C);
I_body[1][1] = mass_vehicle * (A*A + C*C);
I_body[2][2] = mass_vehicle * (A*A + B*B);
```
All other ```I_body``` elements are set to 0.
---
#### Displaced Volume
The displaced volume is the volume that is 1) within the vehicle and 2) within the body of water.

- **```crewModule.dyn.volume_displaced```** (double)
#### Center of Buoyancy
The center of buoyancy is the center of gravity of the displaced volume of water.

- **```crewModule.dyn.center_of_buoyancy```** (double[3])
## Vehicle Shape
In this simulation, the shape of the crew module is defined by a sphere, a cone, and a plane, as shown in the picture below.
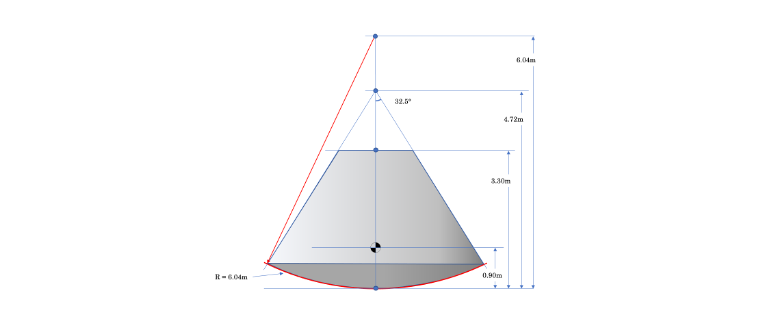
```bool CrewModuleShape::containsPoint(double (&test_point)[3])``` returns ```true``` if the given point is 1) in the sphere, 2) in the cone, and 3) on the correct side of the plane.
The pseudo-function ```inside(double p[3])``` used in the integrals [above](#displaced_volume) represents logic that determines whether a point is within the displaced volume of water. A point is within the displaced volume if 1) it is within the crew module volume, that is ```containsPoint``` returns ```true```, and 2) it is below the surface of the water, that is the z component of the point is less than 0.